Visualise your plotter’s geometry and drawing area#
The drawing area of the potter is determined by its geometry (the length of its arms, the arcs they can sweep through, the relation of those arcs to other aspects of the machine), but the relationship can be hard to understand. Being able to visualise it helps immensely:
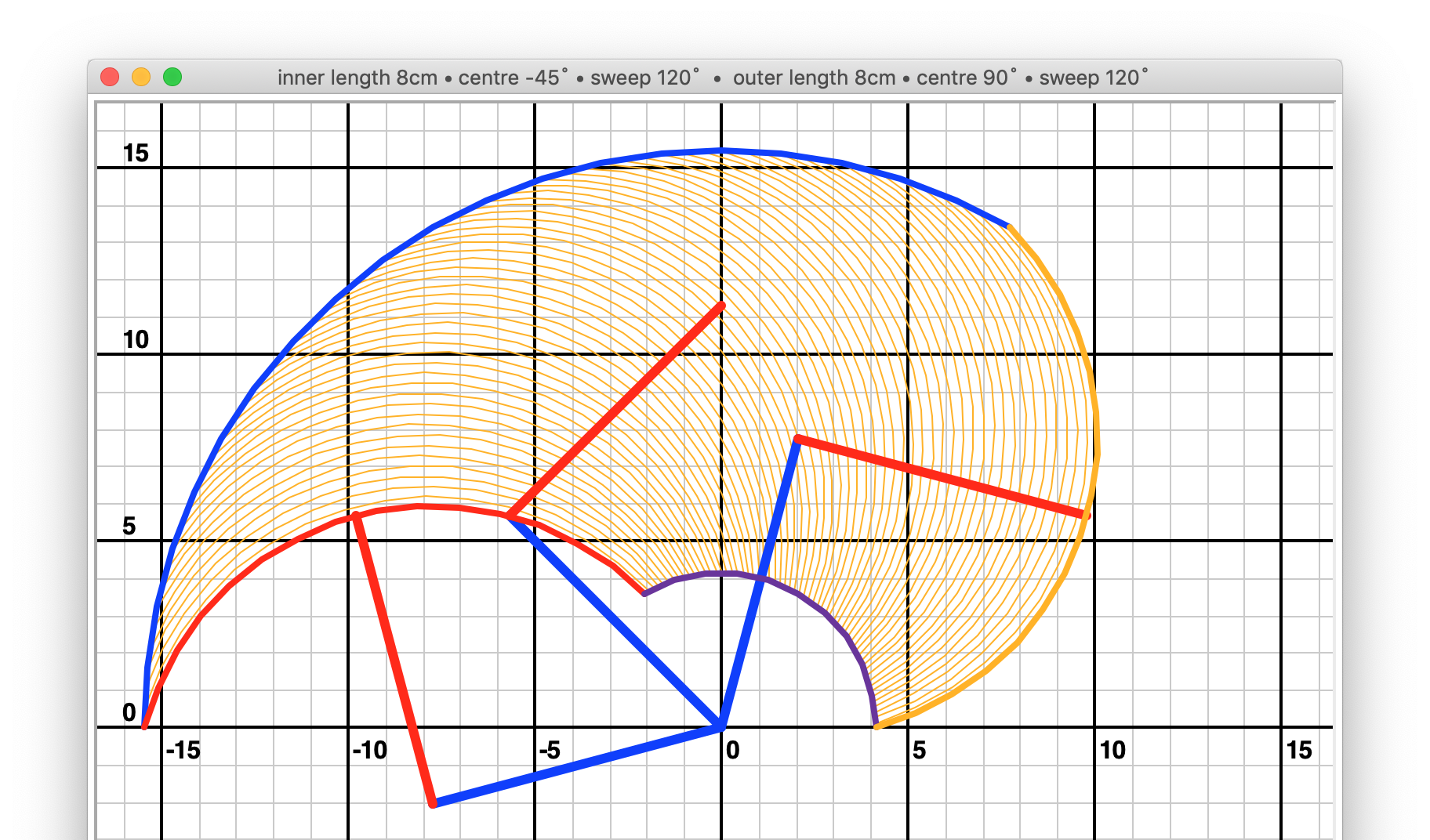
Visualisation is provided by turtle_plotter.py, using Python’s turtle
graphics. Visualisation in turn makes it possible to discover the optimal
plotter geometry. Good plotter geometry means that:
the length of the arms is suited to the power of the motors and the system’s mechanical limitations
you obtain a drawing area that is useful in both size and shape
the movement of the motors to cover that shape is around their centre positions (and not at the extremes of their sweep), and uses not too much or too little of their sweep.
Understanding the plotter’s geometry explores some of the relationships between geometry and plotting area in more detail.
Model a BrachioGraph using turtle_plotter.py#
In a Python shell, import the BrachioGraphTurtle class and instantiate it:
>>> from turtle_plotter import BrachioGraphTurtle
>>> bgt = BrachioGraphTurtle()
BrachioGraphTurtle includes four methods to produce visualisations:
draw_grid()to draw a grid based on the dimensions of the plotter at the moment it was initialiseddraw_arcs()to fill in the drawing area with a series of arcs. These represent sweeps of the outer arm for positions within the sweep of the inner armdraw_arms()to show the positions of the arms at various intervals, to help visualise what the plotter is doingdraw_outline()to trace an outline of the drawing area
Run them to show this plotter’s drawing area:
>>> bgt.draw_grid()
>>> bgt.draw_arcs()
>>> bgt.draw_arms()
>>> bgt.draw_outline()
Customise the model#
As usual in BrachioGraph, nearly all classes can be instantiated without parameters, and working defaults will be applied. These are:
inner_arm: 8
outer_arm: 8
shoulder_centre_angle: 0
shoulder_sweep: 180
elbow_centre_angle: 90
elbow_sweep: 180
Whether you want to model an actual BrachioGraph, or explore a possible one, you’ll need to supply some custom values.
Experience shows that arms of about 8cm work well even with the cheapest of servos, and produce drawings of an adequate size - 14 x 9cm - which works well on sheets of A5 paper.
If you’re modelling an actual plotter, use the actual length of the arms as arguments (note - the length is the distance between its points of rotation).
Real-world servos don’t have sweep angles of 180˚; 120˚ is more realistic (in practice, you may find that your servos have a usable 150˚ sweep).
An example might be:
bgt = BrachioGraphTurtle(inner_arm=8.2, shoulder_centre_angle=-60, shoulder_sweep=120, outer_arm=7.9, elbow_centre_angle=95, elbow_sweep=120)
Close the turtle graphics display before creating a new instance, in order to redraw the grid correctly.
Discover the optimum configuration for your BrachioGraph#
Starting from this point, you can experiment with different values to see how the plotting areas is affected. Typically, given arm lengths and sweep values, you will want to find the centre angles that give the best results (best usually means an outline accomodating the largest useful rectangles for drawing).
As ever, the actual best values will depend on your actual BrachioGraph.
Particularly at the extreme servo angles, or when the outer arm is nearly
inline with the inner arm, you’ll experience poorer control of the pen. The
bounds you provide an actual BrachioGraph need to be based on actual
results as well as theoretical drawing areas.
Use the provided bgt.py module#
As a convenience, the bgt.py module contains a defined
BrachioGraphTurtle instance (this can be more efficient than retyping
values into the shell).
Adjust its parameters appropriately and run python
bgt.py.