The mathematics

The BrachioGraph object contains two trigonometric methods, to translate x/y co-ordinates of the pen into angles of the motors and vice-versa. Using the example illustrated below, the arms are both 9cm long and the pen is at x=4, y=10.

Translating co-ordinates to angles

hypotenuse = math.sqrt(x**2+y**2)
if hypotenuse > self.inner_arm + self.outer_arm:
    raise Exception(f"Cannot reach {hypotenuse}; total arm length is {self.inner_arm + self.outer_arm}")
hypotenuse_angle = math.asin(x/hypotenuse)
inner_angle = math.acos(
    (hypotenuse**2+self.inner_arm**2-self.outer_arm**2)/(2*hypotenuse*self.inner_arm)
)
outer_angle = math.acos(
    (self.inner_arm**2+self.outer_arm**2-hypotenuse**2)/(2*self.inner_arm*self.outer_arm)
)
shoulder_motor_angle = hypotenuse_angle - inner_angle
elbow_motor_angle = math.pi - outer_angle
return (math.degrees(shoulder_motor_angle), math.degrees(elbow_motor_angle))

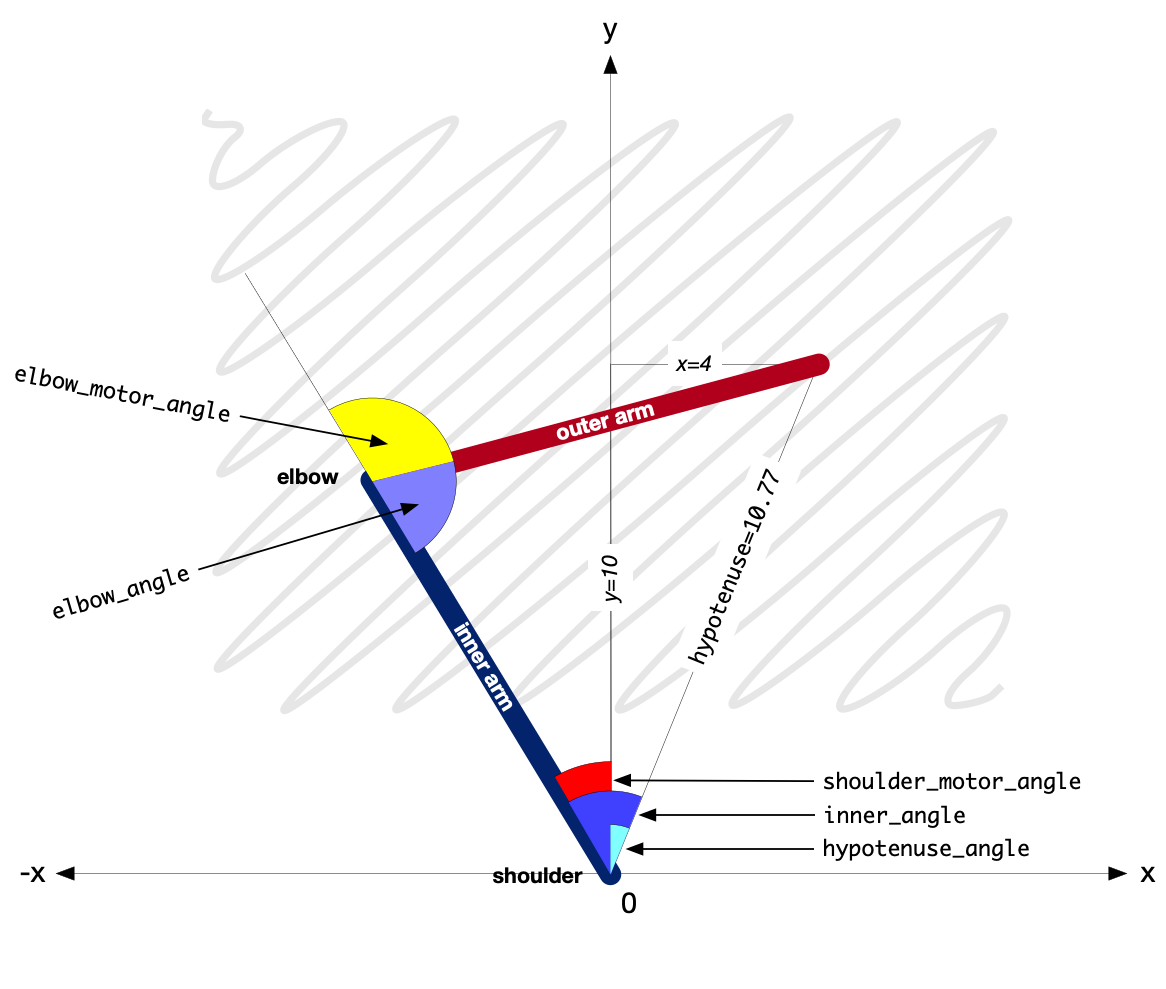
The xy_to_angles() method receives x and y co-ordinates as arguments. First we find a line from the origin (the shoulder motor) to the pen, and its angle from the y-axis:

hypotenuse = math.sqrt(x ** 2 + y ** 2)
hypotenuse_angle = math.asin(x/hypotenuse)

Given x=4, y=10, hypotenuse is 10.77, and its angle from the y-axis (hypotenuse_angle) is 21.8 degrees (0.38 radians).

The hypotenuse line, the inner arm and the outer arm form a second triangle. All their lengths are known, so we can find the angle between the line of the hypotenuse of the first triangle and the inner arm:

inner_angle = math.acos(
    (hypotenuse ** 2 + self.inner_arm ** 2 - self.outer_arm ** 2) / (2 * hypotenuse * self.inner_arm)
)

which is 53.25 degrees. The hypotenuse_angle minus the inner_angle gives us the angle of the shoulder motor (from the y-axis):

shoulder_motor_angle = hypotenuse_angle - inner_angle

in other words, -31.45 degrees. So now we know what angle to set the shoulder motor to.

And similarly, we can find the angle at the elbow, between the inner and outer arms:

outer_angle = math.acos(
    (self.inner_arm ** 2 + self.outer_arm ** 2 - hypotenuse ** 2) / (2 * self.inner_arm * self.outer_arm)
)

The angle of the outer arm relative to the inner arm is 180 degrees (or π radians) minus the outer_angle:

elbow_motor_angle = math.pi - outer_angle

Finally we convert the angle values to degrees and return them:

return (math.degrees(shoulder_motor_angle), math.degrees(elbow_motor_angle))

Translating angles to co-ordinates

Obtaining angles from co-ordinates is essentially the reverse process, in angles_to_xy(). This method isn’t actually used in the BrachioGraph, but can be useful when experimenting.